
Use the grouping information table and tests for differences of means to determine whether the mean difference between specific pairs of groups are statistically significant and to estimate by how much they are different.įor more information on comparison methods, go to Using multiple comparisons to assess the practical and statistical significance. If your one-way ANOVA p-value is less than your significance level, you know that some of the group means are different, but not which pairs of groups. For more information, go to Increase the power of a hypothesis test. Verify that your test has enough power to detect a difference that is practically significant. P-value > α: The differences between the means are not statistically significant If the p-value is greater than the significance level, you do not have enough evidence to reject the null hypothesis that the population means are all equal. For more information, go to Statistical and practical significance.
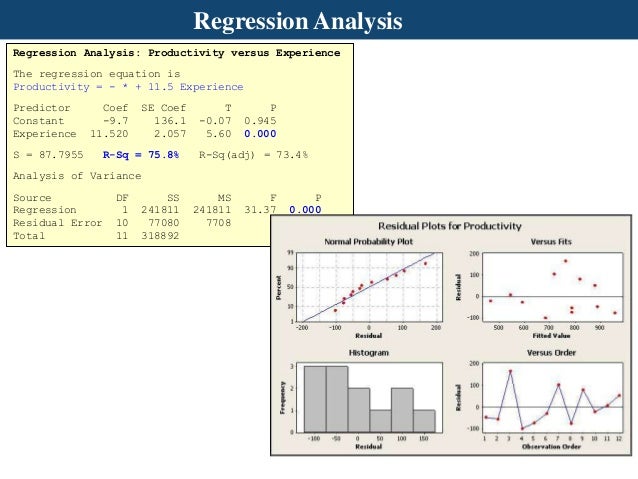
Use your specialized knowledge to determine whether the differences are practically significant. P-value ≤ α: The differences between some of the means are statistically significant If the p-value is less than or equal to the significance level, you reject the null hypothesis and conclude that not all population means are equal. A significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference. Usually, a significance level (denoted as α or alpha) of 0.05 works well. The null hypothesis states that the population means are all equal. this time with the response as weight and the predictor as height*.To determine whether any of the differences between the means are statistically significant, compare the p-value to your significance level to assess the null hypothesis. Now, it's just a matter of asking Minitab to performing another regression analysis. When you select OK, Minitab will enter the newly calculated data in the column labeled height*: Use the calculator that appears in the pop-up window to tell Minitab to make the desired calculation: First, label an empty column, C3, say height*: We can do that using Minitab's calculator. Now, using the fact that the mean height is 69.3 inches, we need to calculate a new variable called, say, height* that equals height minus 69.3. When you select OK, Minitab will display the results in the Session window: Then, select Mean, tell Minitab that the Input variable is height: The easiest way is to ask Minitab to calculate column statistics on the data in the height column. We can first ask Minitab to calculate \(\bar\) the mean height of the 10 students. It's easy enough to get Minitab to estimate the regression equation of the form: Now, as mentioned earlier, Minitab, by default, estimates the regression equation of the form: (The above output just shows part of the analysis, with the portion pertaining to the estimated regression line highlighted in bold and blue.) You may have to page up in the Session window to see all of the analysis. In our case, we again select weight as the response, and height as the predictor: In the pop-up window that appears, again tell Minitab which variable is the Response (Y) and which variable is the Predictor (X). Select Stat > Regression > Regression., as illustrated here: You can find regression, again, under the Stat menu. The second method involves asking Minitab to perform a regression analysis. A new graphics window should appear containing not only an equation, but also a graph, of the estimated regression line:
In our case, we select weight as the response, and height as the predictor: In the pop-up window that appears, tell Minitab which variable is the Response (Y) and which variable is the Predictor (X). Select Stat > Regression > Fitted Line Plot., as illustrated here: You can find the fitted line plot under the Stat menu. Now, the first method involves asking Minitab to create a fitted line plot.
In either case, we first need to enter the data into two columns, as follows: Let's use the height and weight example from the last page to illustrate. There are (at least) two ways that we can ask Minitab to calculate a least squares regression line for us.


 0 kommentar(er)
0 kommentar(er)
